🪴 Quartz 4.0

广度优先「bfs」

3 min read

离开中山路

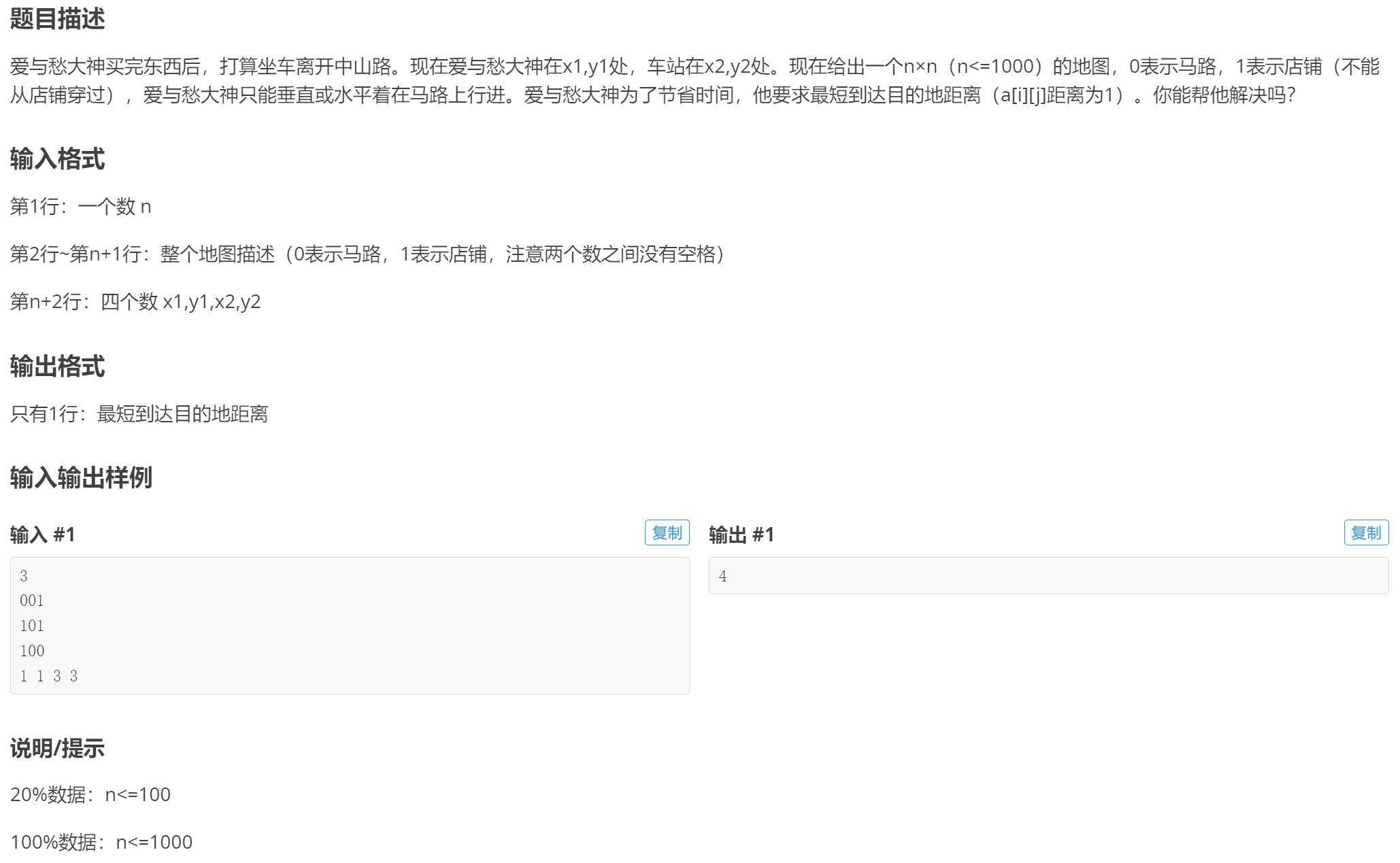解题思路: 步数的统计可以利用状态转移, 然后就是四向广搜, 出界的和查找过的和店铺不搜 ⚠️ c的输入方式跟c++的输入方式不能混用!

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
 
const int maxn=2000;
int a[maxn][maxn];
ll bs[maxn][maxn];
char aa[maxn][maxn];
int n;
int dire[][2]={-1,0,1,0,0,1,0,-1};
int f[maxn][maxn];
 
typedef struct{
	int x;
	int y;
}pos;
pos qi,zhong;
 
queue <pos> q;
 
void bfs(){
	q.push(qi);
	f[qi.x][qi.y]=1;
 
	while(!q.empty()){
		pos t=q.front();
		
		for(int i=0;i<4;i++){
			pos qt={t.x+dire[i][0],t.y+dire[i][1]};
			if(qt.x>=1 && qt.x<=n && qt.y>=1 && qt.y<=n){
				
				if(!a[qt.x][qt.y] && !f[qt.x][qt.y]){
					if(qt.x==zhong.x && qt.y==zhong.y){
						bs[qt.x][qt.y]=bs[t.x][t.y]+1;
						return;
					}else{
						q.push(qt);
						bs[qt.x][qt.y]=bs[t.x][t.y]+1;
						f[qt.x][qt.y]=1;
					}	
				}
			}
		}
		q.pop();
 
//		pos t=q.front();
//		q.pop();
//		if(t.x==zhong.x && t.y==zhong.y) break;
//		if(f[t.x][t.y]) continue;//不重复搜索已标记过的坐标
//		f[t.x][t.y]=1;
//		for(int i=0;i<4;i++)
//		{
//		int tx=t.x+dire[i][0];
//		int ty=t.y+dire[i][1];
//		if(tx>0 && tx<=n && ty>0 && ty<=n && !a[tx][ty])
//		{
//		bs[tx][ty]=min(bs[tx][ty],bs[t.x][t.y]+1);
//		pos qq={tx,ty};
//		q.push(qq);
//		}
//		}
	}
}
 
int main(){
	
//	memset(bs,0x7f,sizeof(bs));
 
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cin>>aa[i][j];
			a[i][j]=aa[i][j]-'0';
		}
	}
	cin>>qi.x>>qi.y>>zhong.x>>zhong.y;
//	bs[qi.x][qi.y]=0;
	
	bfs();
	cout<<bs[zhong.x][zhong.y];
	
	return 0;
}

还有几个点没搞明白

  • 我的做法里min没有意义 “因为你前面已经更新过了”
    • 目前我只知道我的做法里, 快的早就转走了,
  • 但是实测老师的答案不用min和初始化也能过

还可以做一些调整:

  • 比如看老师的答案, 可以有以下改进: 管你什么, 四向都加入队列, 然后在检查点的时候再判断条件, 我原来的答案是先检查条件, 让符合条件的进入队列 (但是超出地图可能需要在加入队列前检查, 不然可能会越界)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
 
const int maxn=2000;
int a[maxn][maxn];
ll bs[maxn][maxn];
char aa[maxn][maxn];
int n;
int dire[][2]={-1,0,1,0,0,1,0,-1};
int f[maxn][maxn];
 
typedef struct{
	int x;
	int y;
}pos;
pos qi,zhong;
 
queue <pos> q;
 
void bfs(){
	q.push(qi);
	f[qi.x][qi.y]=1;
 
	while(!q.empty()){
		pos t=q.front();
		
		for(int i=0;i<4;i++){
			pos qt={t.x+dire[i][0],t.y+dire[i][1]};
			if(qt.x>=1 && qt.x<=n && qt.y>=1 && qt.y<=n){
				
				if(!a[qt.x][qt.y] && !f[qt.x][qt.y]){
					if(qt.x==zhong.x && qt.y==zhong.y){
						bs[qt.x][qt.y]=bs[t.x][t.y]+1;
						return;
					}else{
						q.push(qt);
						bs[qt.x][qt.y]=bs[t.x][t.y]+1;
						f[qt.x][qt.y]=1;
					}	
				}
			}
		}
		q.pop();
 
//		pos t=q.front();
//		q.pop();
//		if(t.x==zhong.x && t.y==zhong.y) break;
//		if(f[t.x][t.y]) continue;//不重复搜索已标记过的坐标
//		f[t.x][t.y]=1;
//		for(int i=0;i<4;i++)
//		{
//		int tx=t.x+dire[i][0];
//		int ty=t.y+dire[i][1];
//		if(tx>0 && tx<=n && ty>0 && ty<=n && !a[tx][ty])
//		{
//		bs[tx][ty]=min(bs[tx][ty],bs[t.x][t.y]+1);
//		pos qq={tx,ty};
//		q.push(qq);
//		}
//		}
	}
}
 
int main(){
	
//	memset(bs,0x7f,sizeof(bs));
 
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			scanf("%c",&a[i][j]);
			a[i][j]=aa[i][j]-'0';
		}
        getchar();
	}
	scanf("%d%d%d%d",&qi.x,&qi.y,&zhong.x,&zhong.y);
//	bs[qi.x][qi.y]=0;
	
	bfs();
	printf("%d",bs[zhong.x][zhong.y]);
	
	return 0;
}

Graph View